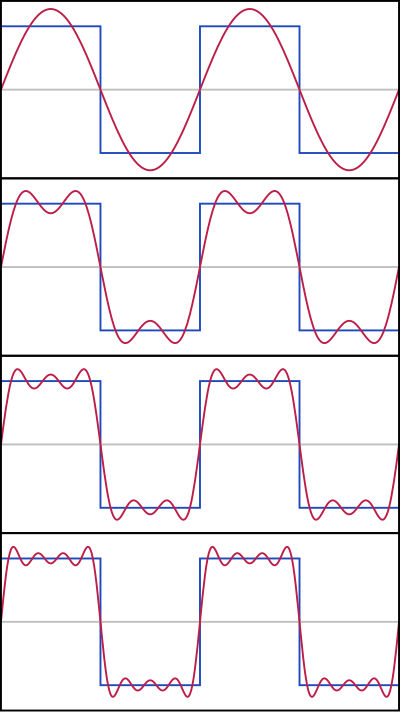
El teorema de Dirichlet es el primer teorema de convergencia puntual de series de Fourier, debido a Dirichlet, apareció en 1829 y se refiere a funciones monótonas a trozos.
Consideraciones previas
Una función monótona y acotada en un intervalo [a,b] es integrable y tiene límites laterales finitos en cada punto. Si estos límites no coinciden la función tendrá una discontinuidad con un salto finito. La suma de los saltos no puede ser mayor que la diferencia de los valores de la función en los extremos del intervalo, de modo que el conjunto de discontinuidades con salto mayor que 1/n es finito y, por tanto, el conjunto de discontinuidades es a lo más numerable. Las mismas propiedades serán ciertas para una función monótona a trozos, es decir, aquella que es monótona en una cantidad finita de intervalos que unidos dan el intervalo original.
Véase también
- Serie de Fourier
Enlaces externos
- Weisstein, Eric W. «Dirichlet Fourier Series Conditions». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Dirichlet conditions en PlanetMath.